РАЗДЕЛ 1

РАЗДЕЛ 1

Глава 1.1

КЛАДЕЗЬ ФОРМАЛИЗМА

Итак, назначение языка – усиливать человеческую мысль. А что можно сказать о его устройстве? Сравнительно недавно, в конце прошлого века, подыскали очень лаконичное и емкое определение: язык – знаковая система.

Знак един в двух лицах: представляет одновременно и себя, и что-то другое. Типичный, хорошо знакомый всем знак языка – слово. С одной стороны, оно указывает на определенный кусочек мира, с другой – само является таким кусочком. Звучащее слово – это колебания голосовых связок, воздуха и барабанных перепонок, последовательность довольно четких, узнаваемых звуков. Еще более осязаемо слово написанное: его можно внимательно рассматривать, держать в руках, даже нюхать.

Способность слова быть указателем – его важнейшая особенность. Но ее внимательное обсуждение мы отложим до третьего раздела. А пока рассмотрим свойство слова быть самим собой. Его часто называют формой, уподобляя слово сосуду, имеющему некое содержание – отсылку к обозначаемому.

Формальное изучение языка было и остается одним из основных занятий лингвистов. К сожалению, слово «формальный» связано в нашем сознании с казенщиной, бюрократизмом и бездушием, вызывает отрицательные эмоции. Немало способствовали этому и многолетние гонения на «формалистов» в искусстве и науке. Между тем буквально слово означает всего лишь «относящийся к форме», и форма может быть неплохой, даже красивой.

Народы во все времена важнейшее значение придавали тому, насколько речь красива внешне. Звуки должны были гармонично сочетаться друг с другом, на стыках слов не рекомендовалось нагромождение труднопроизносимых согласных звуков. Строго относились и к стечениям гласных. Фразы «К отмщенью твоему я, Иоанн, стремлюся» или «сам Блерио у аэроплана», в которых допущено такое скопление (его называют хиатус), нежелательны даже в тексте, не предназначенном для чтения вслух. Вообще, любое повторение одинаковых звуков, если оно не используется как специальный прием, считается нежелательным. Не стоит, скажем, нагромождать одинаковые слоги («Какая река так широка, как Ока») или нанизывать подобные по форме слова («Продолжение наблюдения за проявлением изображения»).

Всегда необходимо различать тончайшие оттенки в произношении звуков. По тому, как человек выговаривает слова, можно очень точно определить, «свой» он или «чужой».

Возникновение такого могучего и влиятельного вида искусства, как литература, непосредственно связано с любованием языковыми формами. Самая главная ветвь (если не ствол) литературы – поэзия – оказывает специфическое воздействие на слушателя или читателя благодаря особой, ритмической форме высказывания. Тесно связанный с поэзией синтетический жанр – песня – все чаще демонстрирует нам, как полностью лишенные содержания, но красивые по форме высказывания приносят удовольствие миллионам людей.

Во всех языках встречается и такое явление, как балагурство. Это естественная, не стесненная рамками правил игра с формами слов. Никакого, казалось бы, смысла нет в нарочитом искажении стандартных речевых форм, но человеку это доставляет удовольствие. Балагур как бы демонстрирует свою власть над языком, хотя, конечно, власть эта имеет пределы – нельзя слишком сильно менять формы, иначе они перестанут служить по назначению.

Изучение тех оболочек, в которых язык хранит свое драгоценное содержание, оказало громадное влияние на логику, а через нее – на все точные науки, включая, конечно, математику. В XX в. логика обрела второе дыхание и легла в основу метаматематики, науки, объединившей слишком далеко расползшиеся ветви математического древа. Методы логики, казавшиеся когда-то пределом абстрактности и заумности, легли в основу вещественных и практичных устройств – компьютеров. Формальные операции, выполняемые ими, – это прямые потомки действий, издревле отточенных на языковых формах.

Постоянное сравнение чистых и гармоничных отвлеченностей, выведенных из наблюдений над этими действиями, с многочисленными неправильностями и нелогичностями языка вынуждало осмысливать противоречие на философском уровне. Действительно, почему язык, будучи по всем внешним проявлениям формальной системой, не доходит в конце концов до предела совершенства? Почему, например, постоянно меняется произношение звуков? Почему одни и те же грамматические признаки выражаются десятками разных окончаний?

Выяснилось, что в языке постоянно действуют две противоположно направленные силы. Одна, «логическая», выравнивает формы, причесывает их, приводит к общему знаменателю, а другая, «волюнтаристская», путает карты и вносит сумятицу. Многовековые наблюдения показывают, что ни одна из этих сил не берет верх, они давно и прочно образуют динамическое равновесие. Нелюбовь людей к абсолютной правильности проявляется даже вопреки их явному желанию быть последовательными. Это хорошо видно на примере специально сконструированных международных языков типа эсперанто. Изначально они делаются сознательно и абсолютно правильно, без каких бы то ни было формальных исключений. Но стоит им только получить распространение, стать средством живого выражения мысли – тут же появляются какие-то диалекты, отклонения от норм, непоследовательности. Это происходит потому, что язык отражает сложный, изменчивый мир через посредство сложных и изменчивых представлений человека, действующего в этом мире. Меняются, колеблются представления, и язык их отражает, перестраивается.

Глава 1.2

КИРИЛЛ, СЕКВОЙЯ И МЕФОДИЙ

Родная стихия всякого человеческого языка – звук. Именно звучащая речь оказалась наиболее удобным способом передачи мыслей. Она позволяет общаться и на расстоянии, и даже когда люди не видят друг друга. При этом не требуется вспомогательных предметов, помощи рук (они часто чем-нибудь заняты), зато используются богатые возможности другого активного органа – языка, который иначе бы бездействовал в долгих перерывах между приемами пищи.

Поскольку звуки, в отличие от изображений, кратковременны, для них очень важно последовательное чередование. Когда люди начали строить язык, они быстро пришли к идее получать множество различающихся последовательностей из очень ограниченного числа акустических элементов. Действительно, во всех известных языках Земли существует по нескольку десятков таких элементов – фонем, и каждое слово – это составленная из них уникальная цепочка. Даже десяти фонем достаточно, чтобы составить миллион отличающихся друг от друга шестизвучных сочетаний. Правда, действительность вносит в это свои коррективы и в несколько раз уменьшает названную цифру, потому что далеко не всякую такую цепочку удобно произносить.

Мысль сделать слово видимым, чтобы придать языку новые возможности, сегодня кажется совершенно естественной и простой. Но подбирались к ней люди чрезвычайно долго. Одни предпочитали ставить вместо слов особые рисунки, почти не связанные с их звучанием. Другие решили применить специальные значки для отдельных фонем или их сочетаний – так возникли алфавиты. Некоторые были созданы сравнительно недавно, и мы знаем даже имена их изобретателей – Месропа Маштоца (армянский алфавит), Кирилла и Мефодия (славянская азбука). Сколь высоко ценятся заслуги создателей письменности, видно хотя бы по тому, что самое величественное дерево планеты – секвойя – названо в честь вождя индейцев чероки Sequo-yah, изобретшего в 1821 г. алфавит племени. В Болгарии, а с недавних пор и у нас ежегодно отмечается национальный праздник – День славянской письменности.

Для многих из нас письменный язык стал эталоном, нормой. По буквам определяем, как слово произносится. Однако буквы в языке (любом) соответствуют фонемам лишь приблизительно. Это объясняется тем, что произношение звуков постоянно меняется и письменность не поспевает за изменениями, продолжает отражать старое звучание. Но есть здесь и положительные стороны: сохраняется традиция; можно исследовать историю развития языка; к тому же закрепленная за словом письменная форма – как бы паспорт, хорошее средство идентификации. Именно поэтому преподаватели языка, лингвисты-ученые, редакторы следят за тем, чтобы пишущие соблюдали грамматические правила; орфографический же словарь – это свод законов, невыполнение которых может привести к неправильной передаче мыслей, недоразумениям.

Поскольку современный человек незаслуженно мало внимания уделяет звукам языка, предлагаем сосредоточиться на них с помощью двух игр.

1.2.1. Поймай звук

Игрокам понадобится звучащая речь; для этого можно использовать радио, телевизор, магнитофон или попросить кого-нибудь почитать вслух книгу.

Договариваются об объекте ловли. В первом варианте игры это должен быть редкий звук языка, например ш, ц, з, х. По сигналу начала игры все внимательно вслушиваются в речь. Тот, кто услышал заданный звук, как можно быстрее повторяет слово с ним. Ему, опередившему остальных, присуждается очко. Выигрывает тот, кто первым наберет десять очков.

Необходимо помнить, что звук и буква – не одно и то же. Например, букву ф почти не употребляют, но звук ф довольно часто встречается в речи при оглушении в; буква ь существует, звука же ь нет, букве ю соответствуют два звука: й и у.

Если редкий звук используется в одном-двух часто повторяющихся фрагментах (словах, окончаниях), имеет смысл ввести дополнительное условие: штраф за слова с такими фрагментами. Для звука ш это будет слово что, для звука б – различные формы глагола быть, для х – падежные окончания множественного числа некоторых существительных... Штраф означает отнять одно из заработанных очков, если таковые есть; если их нет, то действует правило «с нищих не берем».

Рекомендуем также второй вариант с «поимкой» не отдельных звуков, а звукосочетаний или целых слов: что, не, это и т. п.

1.2.2. Искусственный акцент

Участники игры договариваются в течение какого-то времени вносить в свою речь искажения по заданному правилу.

В первом варианте все слова (за исключением односложных) произносят с неправильным ударением. Игроки ведут беседы, задают друг другу вопросы и стараются поймать собеседника на невыполнении условия. За слово со словарным ударением начисляется штрафное очко. Отмалчиваться не разрешается, нужно активно поддерживать разговор. Побеждает тот, у кого будет меньше штрафов. Можно играть и «на вылет», до первой ошибки (т. е. правильности), пальма первенства достается оставшемуся. Этот вариант естественно назвать «Неправильные ударения».

Во втором варианте искаженно произносятся все слова с ударениями на звуках о или а. Ударные а следует заменять ударными о. И наоборот. Вместо собака произносится собока, вместо корова – корава. Подобным же образом вертолет превращается в вертолят, пять – в петь. Штрафные очки начисляются так же, как и в предыдущем случае.

В третьем варианте каждый глагол следует ставить в неопределенную форму. Особенно внимательно нужно следить за вспомогательным глаголом быть, который участвует в образовании сложных форм:

– Ты быть пить чай?

– Спасибо, не быть, я уже пить.

Можно придумать и другие искажения.

Знать, как пишется слово, – необходимость для культурного человека. И здесь неоценимую помощь оказывают формальные игры на построение цепочек букв. Основная операция в них – найти правильную, т. е. одобренную словарем или признанным авторитетом, цепочку по некоторым (заданным) буквам.

В таких играх (назовем их орфографическими) во избежание неясностей и разногласий надо заранее оговорить, какой словарь будет служить эталоном. Удобнее всего пользоваться полным орфографическим словарем русского языка. Если решили употреблять как игровой материал имена собственные, понадобится энциклопедический, биографический или топонимический (содержащий названия географических пунктов) словарь. Те, кто хорошо разбирается в какой-то специальной области, могут воспользоваться словарем профессиональных терминов.

Вот пример традиционной орфографической игры, различные варианты которой общеизвестны.

1.2.3. Подбор

За определенное время нужно подобрать как можно больше слов по заданному формальному условию. Время в зависимости от сложности условия колеблется в пределах 3–10 минут.

В различных вариантах этой игры задаются:

а) одна или несколько первых букв (иногда с указанием длины слова);

б) одна или несколько последних букв;

в) рифма;

г) первая и последняя буквы;

д) некоторые буквы с указанием их позиций. Например, в игре «Сквозная буква» нужно подбирать слова, в которых на втором (третьем, четвертом...) месте стоит одна и та же буква;

е) цепочка букв, которая может стоять в любом месте слова;

ж) перечень согласных букв слова;

з) полный набор согласных букв слова с указанием их последовательности (этот вариант носит название «Каркас»);

и) полный набор гласных букв слова с указанием их последовательности;

к) единственная гласная буква, которая может употребляться.

Обращаем внимание читателя на то, что при обозначении последовательных пунктов буквами алфавита, как это сделано выше, не принято использовать не только букву ё, об особенном положении которой здесь уже говорилось, но и й.

Все десять вариантов игры можно проводить и по другой схеме: дается несколько однотипных заданий, и победителем становится тот, кто их раньше выполнит. Для варианта г (первая и последняя буквы) набор заданий обычно состоит из одного слова, записывают его по вертикали дважды – сверху вниз и снизу вверх, например:

И . . . . . А

Г . . . . . Р

Р . . . . . Г

А . . . . . И

Кто быстрее заполнит промежутки между буквами, тот и победил.

Задание 1.2.3.1. Не ограничивая себя во времени, подберите как можно больше слов, начинающихся со следующих буквосочетаний: дж... (41), ес... (23), куз... (16), лы... (17), мос... (33), мр... (12), ущ...(17), хм... (21), яг... (26).

В скобках указано количество слов с таким началом в «Орфографическом словаре русского языка» под редакцией В. В. Лопатина (М., 1991). Сложите свои результаты и отдельно – соответствующие им суммы по словарю. Разделив первое число на второе и умножив частное на сто, получите выраженный в процентах коэффициент активного освоения вами лексики.

Задание 1.2.3.2. Аналогично предыдущему подберите слова, заканчивающиеся на ...ыв (19), ...вье (14), ...рье (17), ...еж (16), ...аг (19), ...ег (13), ...рд (23), ...ык (18). В скобках указано, сколько таких слов можно найти в «Грамматическом словаре русского языка» А. А. Зализняка (М., 1977).

Подсчитайте коэффициент активного освоения лексики так же, как и в предыдущем задании, сравните оба коэффициента. Если они различаются, то почему?

Задание 1.2.3.3. Вставьте пропущенные буквы так, чтобы получилось восемь семибуквенных существительных. Дополнительное условие – четыре пары рифм:

П . . Е . . Т . А . А . . А

С . М . Л . Т К . Б . Н . А

. О . Н . . Т С . Р . Л . К

Т . Н . И . Т С . И . Т . К

Наверное, разгадке поможет такая информация: задание предлагалось на детском военно-физкультурном празднике, посвященном 20-й годовщине РККА (1938 г.)

Если условие настолько легкое, что нужные слова находятся почти мгновенно, форму игры можно сделать более динамичной.

1.2.4. Верни с ответом

Игроки становятся в шеренгу. Ведущий – ему потребуется мяч или другой предмет – лицом к ним. В первом варианте игры он громко произносит какой-нибудь слог и бросает мяч вперед. Поймавший должен не мешкая кинуть его обратно, добавив к слогу продолжение, чтобы при этом получилось слово. Если игрок повторил уже произнесенное кем-то или просто замешкался, он отходит в сторону. Темп все убыстряется, до тех пор пока в шеренге не останется один – победитель; его можно назначить ведущим в следующей игре.

Желательно подбирать такие слоги, с которых начинается достаточно много слов. Скажем, взять часто встречающуюся согласную (к, л, м, н, п, р, с, т) и добавлять к ней гласные. Это проще всего. Кинуть мяч нужно так, чтобы для игрока этот бросок был внезапным и чтобы игроки находились в равных условиях.

Во втором варианте игры называется не слог, а целое слово. Задача игрока, которому брошен мяч, – назвать рифму к этому слову. Ведущему стоит заранее, до игры, подобрать и записать несколько десятков существительных, к которым не составит особого труда найти рифмы. Хорошо, если ведущим способен быть каждый из играющих. Для подбора рифм удобно использовать обратный словарь, где слова упорядочены по последним буквам.

Игровое задание может быть и обратным: дается слово, и над буквами, из которых оно составлено, следует произвести определенное действие, получив, быть может, бессмысленную цепочку букв.

1.2.5. Слово наизнанку

Ведущий громко и внятно называет какое-нибудь слово. В первом варианте игры остальные должны в уме представить, как это слово читается наоборот, от конца к началу. Например, услышав телеграф, надо мысленно прочитать фаргелет и произнести полученный перевертыш. Если нет ошибки (ведущий проверяет это по своим записям), опередивший всех игрок зарабатывает очко; если ошибся – у него отнимается очко из числа набранных. Выигрывает тот, кто первым наберет 10 очков.

Следует помнить, что в обратном порядке ставятся буквы, а не звуки: яд превращается в дя, а не в тай. Мягкий и твердый знаки игнорируются.

Естественно, переворачивать длинные слова труднее. Ведущий подбирает их в зависимости от возраста и уровня развития игроков, чтобы времени на размышление требовалось не очень много (и не слишком мало).

Во втором варианте игры (упрощенном) нужно переставлять в обратном порядке не отдельные буквы, а целые слоги (тот же телеграф превратится в графлете). Подбирая слова подлиннее, ведущий может использовать словарь.

Преобразование слова в бессмысленную цепочку букв и последующее восстановление его из этой цепочки можно объединить в одной игре.

1.2.6. Анаграммы

Первый вариант: ведущий (в его роли может поочередно выступать каждый игрок) задумывает какое-нибудь слово и записывает ясно и разборчиво анаграмму, т. е. все составляющие его буквы в другом порядке на бумаге или доске. Сколько раз буква встречается в слове, столько раз ее и надо написать. Тот, кто первым восстановит правильную последовательность, зарабатывает очко. Игра ведется до тех пор, пока кто-нибудь не наберет заданное количество (5–10) очков. Для удобства их подсчета имеет смысл каждую анаграмму записывать на отдельном листке и отдавать его отгадавшему.

Естественно, длина слов зависит от возраста участников. Для маленьких детей годятся трех-четырехбуквенные анаграммы, взрослые разгадывают и восьмибуквенные. Впрочем, сложность не всегда зависит от длины слова: облегчают отгадывание стандартные суффиксы и редко встречающиеся буквы.

Если под рукой окажутся карточки или фишки с написанными на них отдельными буквами, советуем ими воспользоваться: легче станет перемешивать и показывать анаграммы, уменьшится вероятность ошибки.

Рекомендуем и несколько отличающийся второй вариант игры: для двух человек, в котором соперники одновременно предлагают друг другу разные анаграммы с одинаковым количеством букв. Побеждает тот, кто первый справится с задачей (при этом он обязан сообщить решение придуманной им анаграммы своему противнику).

Еще один вид игровых преобразований – переход от одного слова к другому по формальному правилу. Обычно строится цепочка таких переходов. Ее можно перекидывать от игрока к игроку, а можно попытаться связать ею и два заданных слова.

1.2.7. Метаграммы

Первый вариант игры: задаются два четырехбуквенных слова. Нужно перейти от одного слова к другому за несколько шагов, меняя на каждом шаге только одну букву. При этом все получающиеся цепочки букв должны быть существующими в языке словами. Например, сено за четыре шага превращается в ноль:

сено – село – соло – соль – ноль

Если в исходных словах не совпадают буквы, стоящие на одинаковых местах, то наименьшее возможное количество шагов – четыре.

Выигрывает тот, кто первым сумеет построить соединительную последовательность. Поскольку найти ее можно далеко не для каждой пары, имеет смысл задавать не два слова, а больше, тогда побеждает сумевший первым соединить любые два слова из этого набора. Если на игру отвести много времени, то определять победителя можно по другому принципу: кто найдет более короткую последовательность слов для соединения.

Автором этой игры считается Л. Кэролл, автор «Алисы в стране чудес».

Существует второй вариант, в котором разрешается не только заменять буквы, но и добавлять или убирать их по одной за каждый шаг (при том же условии правильности получающихся слов). В этом варианте можно задавать исходную пару с разным количеством букв. Например, кот и спор:

кот – корт – порт – спорт – спор

Естественно, далеко не всякие слова можно соединить даже при таком условии. Поэтому существует еще более смягченный третий вариант: на каждом шаге можно не только менять одну букву, но и переставлять буквы по принципу анаграммы.

Задание 1.2.7.1. Соедините цепочкой метаграмм слова муха и слон.

Головоломки типа метаграмм или анаграмм часто публикуются. Нередко в них задаются слова, так или иначе связанные по смыслу (например, как в только что приведенном задании, с противоположными значениями). Это никак не связано с лингвистическим содержанием игры, в таких случаях она остается чисто формальной. Единственное назначение подобных псевдосемантических добавок – придать игре определенное эстетическое качество.

1.2.8. Чайнворд

Эта игра похожа на «Метаграммы». Так же задаются два слова и требуется построить цепочку слов для перехода от одного к другому. Но здесь звенья в цепочке связываются по правилу: последние буквы предыдущего слова должны совпадать с первыми буквами последующего. Есть два основных варианта условия: первый вариант – совпадать должны ровно две буквы, второй вариант – не менее чем две. Второй вариант мягче, но и первый дает значительно больше возможностей для связывания, чем метаграммы. Например:

стул – улика – карьерист – стол

Если не предъявлять заведомо невыполнимые задания (скажем, перейти от демиурга к чреву), то за 3–5 минут, как правило, можно найти не одну соединительную цепочку. Поэтому выигравшим считается тот, кто сумел обойтись наименьшим количеством звеньев.

Существует более простой третий вариант игры, в котором строится цепочка слов, где каждое начинается с последней буквы предыдущего (или с предпоследней, если слово кончается на ы или ь). Задача связать два заданных слова решается при таком условии легко, поэтому здесь строят бесконечную цепочку. Участники по очереди добавляют новые звенья. Проигрывает тот, кто не может назвать очередное слово, не повторив уже названные. Этот вариант хорошо известен под названием «Города» (разрешается использовать названия населенных пунктов).

Игра «Чайнворд» больше известна как головоломка с использованием не только формальных, но и смысловых условий, поэтому упоминание о ней встретится в следующем разделе (см. игру 3.4.8 – «Кроссворд»).

Задание 1.2.8.1. Найдите кратчайший путь от слова муха к слову слон:

а) так, чтобы у соседних слов в цепочке было не менее чем по две связующие буквы;

б) так, чтобы у соседних слов было ровно по две связующие буквы.

В следующих двух знаменитых играх используются известные нам по игре «Подбор» переходы от набора букв к слову, но здесь уже игроки действуют не изолированно. Каждый имеет возможность осложнить задачу соперника и это придает соревнованию больше развлекательности.

1.2.9. Виселица

Играют вдвоем. Один задумывает слово и записывает на листке его первую и последнюю буквы, ставя точки вместо остальных. Задача второго участника этого состязания – угадать слово. Он может назвать любую букву алфавита и спросить, есть ли она в задуманном слове. Если ответ утвердительный, буква ставится вместо точек. Если отрицательный, – штрафное очко. Чем больше задано вопросов, тем больше сведений о слове. Но при этом больше и штрафных очков. Устанавливается их критическое число, обычно 10–20. Если оно набрано, это означает проигрыш отгадчика. В следующем туре отгадывающий и загадывающий меняются ролями. И так до определенного количества побед.

Название объясняется оригинальным способом подсчета штрафных очков. В ответ на каждый неудачный вопрос загадавший рисует часть схематического изображения виселицы с болтающимся на ней человечком: перекладины, веревку, голову, туловище... Если дорисовывается последний фрагмент этого зловещего изображения, слово считается неразгаданным.

1.2.10. Балда

Обычно соревнуются двое, но можно играть и втроем, и вчетвером. Устанавливают очередность ходов, первый игрок называет любую букву. В первом варианте игры каждый последующий ход заключается в добавлении одной буквы справа или слева, причем запрещается создавать сочетания, не встречающиеся в русском языке. Если игрок образовал законченное слово или не смог придумать подстановку, он получает штрафное очко.

Игра продолжается до тех пор, пока кто-нибудь не наберет пять штрафных очков.

Название объясняется способом фиксации очков: они последовательно обозначаются б, а, л, д, а. Проигрывающие постепенно набирают буквы, составляющие это обидное слово.

При всей своей незатейливости игра заслуженно является классической, потому что требует умения охватить множество вариантов, богатого словарного запаса и, кроме того, довольно азартна. Подобно шахматам, в ней есть теория дебютов: например, известны проигрышные буквы, начинать с которых не рекомендуется.

В усложненном втором варианте разрешается подставлять очередную букву не только в начале или конце цепочки, но и внутри. Это, естественно, расширяет возможность поиска.

Для мастеров игры предлагается третий вариант – «Супербалда», где буквы можно менять местами, т. е. использовать анаграммы.

Существует и четвертый вариант – «Антибалда»: тот, кто первым получает законченное слово, зарабатывает не штрафное, а выигрышное очко. Начав с одной буквы, можно набрать несколько очков, пока не будут исчерпаны возможности продолжения.

Задание 1.2.10.1. Найдите проигрышные буквы, с которых не стоит начинать игру «Балда». Для этого потребуется подобрать и исследовать множество слов с редкими двухбуквенными сочетаниями.

Задание 1.2.10.2. Найдите запрещенные двухбуквенные сочетания, не встречающиеся в русских словах.

Глава 1.3

ЛЫКО В СТРОКУ

Слова составляются из звуков, предложения – из слов, тексты – из предложений. Здесь все построено на разнообразии комбинаций, можно даже сказать, что сочетания – душа языка. Умение быстро строить одну за другой конструкции из заданного набора элементов отличает человека, хорошо владеющего языком. К числу наиболее привлекательных относятся игры, в которых необходимо мысленно создать множество сочетаний из заданного набора букв и выбрать правильные, т. е. соответствующие словам.

Игры с перебором комбинаций спортивны по своему характеру, здесь важна скорость просмотра, зоркость и точность в определении слова, спрятавшегося в хаосе бессмысленных цепочек букв.

1.3.1. Наборщик

Называется слово. В течение 10–15 минут нужно составить как можно больше слов из его букв. Оно служит как бы типографской кассой, из которой вынимаются литеры и возвращаются обратно после набора каждого очередного слова. По истечении времени каждый зачитывает свои слова, и если у других встречаются такие же, они вычеркиваются у всех. Выигрывает тот, у кого останется больше слов.

Длина исходного слова зависит от уровня подготовленности участников: начинающим нравятся наборы из 15 и более букв, для опытных игроков интереснее кассы покороче. Обычно договариваются подбирать слова не менее чем из 4–5 букв.

Можно применить и более длинный исходный набор (с помощью нескольких слов или россыпью в виде двух-трех десятков случайных букв). Задание здесь сложнее: составить как можно более длинный ряд слов, используя буквы без возврата в кассу.

Игра «Наборщик» (другие названия – «Колбаса», «Навуходоносор») очень популярна, потому что всякий раз позволяет задеть новый пласт словаря, совершить маленькие открытия.

Задание 1.3.1.1. Дана россыпь из 32 букв. Составьте несколько слов, в которых используется весь алфавит, причем каждая буква по одному разу.

Задание 1.3.1.2. Прочитайте вслух латинские слова:

Впрочем, два из них – русские и даже написаны по-русски, но их можно прочесть и на иностранный манер, так как в нашем языке многие буквы похожи по начертанию на латинские. Возникающих при этом слов купон и реникса в латинском языке нет. Однако среди двоякочитаемых найдутся и вполне «законные» в обоих языках. Поскольку многие читатели владеют английским, предлагаем найти слова, которые по-своему прочтут и поймут и русский, и англичанин.

Интересно, что задача поиска русских слов, которые пишутся латинскими буквами, обретает неожиданный практический смысл для программистов, которые хотят что-нибудь написать по-русски на «нерусифицированном» компьютере.

1.3.2. Словарь-смекалка

Потребуется набор букв на отдельных фишках или карточках, в котором количество экземпляров одной буквы тем больше, чем она употребительнее. Фишки рассыпают буквами вниз и, открывая по одной, через определенные промежутки времени кладут в центре стола. Кто первым сумеет составить слово, называет его вслух; необходимые для этого фишки забирает и раскладывает перед собой так, чтобы видели остальные игроки.

Для составления слова можно использовать буквы не только с центра стола, но и из слов, уже разложенных перед кем-то. Однако буквы чужого слова должны быть использованы все до единой за один раз. Например, у кого-то есть двор, а вы заметили, что в центре появилась буква е, – берете это слово и, добавив е, выкладываете перед собой ведро. Или так: у соседей есть след и пиво; добавив е, получите велосипед. Разрешается составлять сразу несколько слов: скажем, у соперника набран оркестр, а в центре стола – с и а; вы можете создать из этого для себя слова треск и роса.

Повторяться нельзя. Побеждает тот, кто первым составит 10 слов. Для усложнения игры можно договориться не использовать слова короче 5–6 букв.

Соревнование это динамично, азартно, лидерство нередко переходит из рук в руки, потому что накопленное вами может быть в любой момент захвачено конкурентом.

Более сложными становятся условия, если слова соединяются друг с другом и, пересекаясь, образуют пространственную сеть. Судя по той популярности, которой пользуются игры с переплетениями слов типа кроссворда, за ними стоит нечто большее, чем просто интересная искусственная форма. Не исключено, что в мозгу подобным сетям соответствуют определенные переплетения нейронов. Это, во-первых, дает некоторую экономию (одна буква участвует в составлении сразу нескольких слов) и, во-вторых, позволяет путешествовать в словарном пространстве.

1.3.3. Крестословица

Для игры потребуется игровое поле – квадрат 15 x 15 клеток – и набор фишек с написанными на них буквами. Каждая буква имеет «цену», зависящую от частоты ее употребления: чем реже встречается, тем дороже стоит, соответственно набор фишек для игры делают таким, чтобы в нем было больше общеупотребительных букв. Сюда включают также две или три фишки-«звездочки», которые могут представлять по желанию игрока любую букву. Стандартный набор для игры приведен в таблице:

В первом варианте игроки берут себе наугад по 7 фишек. Ходят по очереди, выставляя любое количество своих фишек на поле так, чтобы они вместе с размещенными ранее буквами образовали новые слова, идущие слева направо или сверху вниз. Нельзя ставить фишки, если при этом образуется хотя бы одно бессмысленное слово. Тот, кто не может ничего придумать, пропускает ход, а кто выставил несколько фишек, добирает себе столько же из общего набора. Сумма цен всех выставленных букв дает выигрышные очки, поэтому выгоднее подыскивать слова с редкими буквами. Кроме того, некоторые клетки (их помечают разными цветами) удваивают или утраивают стоимость буквы или всего проходящего через них слова.

Игра эта, известная на Западе под названием «Скрэбл» («Scrabble»), появилась на русском языке в начале 60-х годов и с разработкой промышленных комплектов «Эрудит» быстро завоевала популярность.

Недостаток этого варианта: победа нередко зависит от случая – насколько удачные выпадут буквы.

Поэтому рекомендуем второй вариант, в котором все игроки находятся в равных условиях. Каждый раз берут одну на всех игроков семерку букв и ставят таймер на 3 минуты; мысленно за это время располагают фишки наиболее выгодным образом, затем подсчитывают и называют соответствующие очки. На поле выставляется самое ценное решение, а записывает себе каждый ту сумму, которую назвал.

Стандартное поле для игры выглядит так:

Условные обозначения:

0 – клетка первого хода

2б – удвоение буквы

3б – утроение буквы

2с – удвоение слова

3с – утроение слова

1.3.4. Формальный кроссворд

Все вместе придумывают «плетенку» – фигуру из пересекающихся под прямым углом полосок одинаковой ширины, поделенных на квадраты. Каждый изображает ее на своем листке (лучше использовать бумагу в клеточку). Простейшие фигуры можно образовать, например, четырьмя полосками; чтобы не возникало путаницы, изолированные внутренние квадраты заштриховываются:

Более сложные переплетения – из пяти и шести полосок:

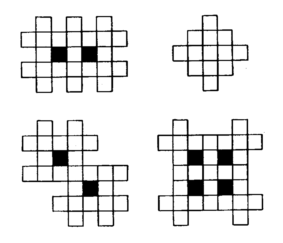
Когда фигура придумана, участники игры пытаются заполнить всю ее (по одной букве в клетке) так, чтобы на каждой горизонтальной полоске от левого края до правого, а на каждой вертикальной от верха до низа можно было прочесть какое-то слово.

Выигрывает тот, кто раньше других правильно выполнит задание. Может получиться так, что переплетение слишком сложно и поставить слова всюду не удается. В этом случае через определенное время (по договоренности) игру останавливают и победителем становится тот, кто впишет больше букв.

Игру можно провести и иначе. После заполнения «плетенки» каждый загадывает свой вариант, указав только первую и последнюю буквы слова. Первый, кто заполнит фигуру при этих ограничениях, зарабатывает очко.

В такой модификации игра напоминает разгадывание традиционного кроссворда (о нем еще пойдет речь в главе 3.4), но на совершенно формальных условиях.

Конструирование кроссвордов – занятие не менее увлекательное, чем их разгадывание. От количества взаимных пересечений полосок, естественно, зависит трудность подбора слов. Однако работа составителя в среде профессионалов оценивается не только по плотности переплетения, но и по связности кроссворда, его симметричности. Связность – показатель единства различных частей фигуры, их взаимопроникновения. Требование симметричности возникает из чисто эстетических соображений и заставляет задуматься, не имеем ли мы дело с видом искусства. Что же касается размера, то известны рекордные кроссворды, на составление которых уходят годы труда.

Если отказаться от орнаментальности, то фигуру из полосок (необязательно прямоугольных) можно сделать похожей на какой-то реальный объект. Это свойство обыграно писателем Ю. Буковским в «Кактусвордах», появлявшихся на страницах детского журнала «Искорка».

Задание 1.3.4.1. Заполните по правилу кроссворда эти квадраты:

Глава 1.4

ОТ ТЬМЫ ДО АСКИ-КОДА

Как уже говорилось, язык действует по принципу моделирования; с его помощью строятся знаковые подобия вещей и явлений. Жизнь слов – это отражение жизни реального мира. Есть и еще одна общеупотребительная модель, вполне самостоятельная, по-своему отражающая мир – математическая. Каждый человек умеет пользоваться числами, знает определенные законы математической логики, владеет геометрическими представлениями.

Конечно, две такие влиятельные знаковые системы не могли не вступить в контакт. Особенно способствовала ему письменность. Буквы оказались великолепными математическими объектами: никакой расплывчатости, ограниченный набор элементов, бесконечное множество комбинаций. В сопоставлении языка и математики первый кажется предназначенным для более возвышенных целей. Это ощущение выразил Н. Гумилев:

А для низкой жизни были числа,

Как домашний подъяремный скот,

Потому что все оттенки смысла

Умное число передает.

Доказательством издавна существовавшего взаимопроникновения математики и языка служит то, что у всех народов буквы первоначально использовались и для обозначения чисел. В старинной русской азбуке числа в пределах тысячи обозначались буквами со знаком титла сверху:

Для обозначения тысяч к букве дополнительно присоединялся слева знак , например:

Большие числа записывались двумя способами. По системе «великого числа»:

По системе «малого числа» тьма означала 10⁴, легион – 10⁵, леодр – 10⁶.

К сожалению, нашим предкам очень трудно было производить математические операции с числами, записанными в подобной системе. Неудобства испытывали и те, кто пользовался римскими цифрами-буквами I, V, X, L, C, M: даже для простого деления требовалось высшее образование. Конечно, неудобства были вызваны не какими-то присущими буквенным символам недостатками, а формой записи. Общеупотребительные ныне арабские цифры тоже произошли от букв. Отголосками древнерусской системы числовых обозначений дошли до нас лишь выражения «народу – тьма» и «имя им – легион».

Но вот появились компьютеры, и вновь встал вопрос о буквенно-числовых соответствиях. Теперь, правда, роли переменились: требовалось обозначать буквы с помощью чисел, чтобы машина могла их запоминать и манипулировать ими. Довольно скоро программисты пришли к соглашению о стандартах на такие обозначения. Латинским буквам больше повезло, потому что специальные языки для общения с компьютером разрабатывались обычно на основе английского. Сейчас во всем мире приняты так называемые АСКИ-коды (от сокращения ASCII – American Standard for Computer Information Interchange). С их помощью можно обозначить 256 различных символов, что позволяет представить сразу несколько алфавитов – латинский, какой-либо национальный и плюс к ним набор специальных символов, знаков пунктуации, математических знаков и т. п. Кстати, пробел между словами – тоже машинный символ, имеющий свои числовой код – 32. К сожалению, кириллическая азбука пока что неуютно устроилась в АСКИ-ложе, существует по крайней мере шесть разных стандартов записи, и у каждого из них есть недостатки. Вот лишь один, так называемый альтернативный вариант ГОСТа, получивший большое распространение:

прописные от А до Я: коды 128–159

строчные от а до п: коды 160–175

строчные от р до я: коды 224–239

буквы Ё и ё: коды 240, 241

Как правило, числовые коды подбирают так, чтобы их возрастание соответствовало порядку букв в алфавите. Это существенно облегчает одну из наиболее традиционных задач – упорядочение слов. Правило словарного порядка известно всем: из двух слов вначале ставится то, у которого первая буква идет в алфавите раньше, если совпадают первые буквы, то сравниваются вторые и т. п.

Для игр со словами удобнее всего поставить в соответствие каждой букве ее порядковый номер в азбуке. С помощью номеров слова легко превращаются в числа, а числа – в слова, что открывает богатые игровые возможности.

1.4.1. Гемтрия

Выбирают слово и подсчитывают сумму алфавитных номеров составляющих его букв. После этого каждому игроку предлагается за определенное время (20–30 минут) найти как можно больше слов с такой же суммой. По истечении времени одинаковые слова вычеркиваются; выигрывает тот, у кого останется больше незачеркнутых.

Для удобства необходима, конечно же, таблица номеров: а – 1, б – 2 ... я – 32 (помните, что ё равно е). Время игры может быть и больше, просматривается громадное количество вариантов. Способы просмотра совершенствуются с каждым новым заданием, поэтому игровой опыт здесь много значит.

Название игры взято из Каббалы, средневекового мистического учения. Гемтрия – это поиск слов и их сочетаний с заданными числовыми показателями. Предполагается, что слова, у которых показатели равны, имеют важную смысловую связь.

Описание практической гемтрии содержится в одном из эпизодов романа Л. Толстого «Война и мир». Пьер Безухов узнаёт, как с помощью французской азбуки масоны интерпретируют «звериное число» 666, упоминаемое в Апокалипсисе. В соответствии с традицией буквенного представления чисел первыми девятью буквами (a – i) обозначаются единицы, прочими – десятки: k – 10, l – 20, m – 30 ... z – 160. Удается найти два словосочетания с нужной суммой:

Первое из них означает «император Наполеон», второе – «сорок два». Объяснение простое: когда императору исполнилось сорок два года (также апокалипсический возраст), наступил предел его власти.

Пьер проделывает собственные вычисления и открывает, что словосочетание Le Russe Besuhof (русский Безухов) составляет 671 очко. Отбросив e в артикле, он получает слегка искаженное грамматически выражение для «звериного числа». Отсюда его не совсем логичный вывод, что именно он положит предел власти Наполеона.

Задание 1.4.1.1. Найдите как можно больше слов в русском языке, дающих ту же сумму номеров букв, что и слово игра (31).

Задание 1.4.1.2. Найдите четырех- и пятибуквенные слова с наибольшей суммой номеров букв.

Задание 1.4.1.3. Найдите как можно больше слов, в которых буквы следуют в порядке строгого возрастания номеров (таковы, например, век, дело, гостья).

Не только арифметика, но и другие разделы математики тесно связаны с языком. Поскольку написанное слово обычно представлено на плоскости, оно обладает определенными геометрическими свойствами. Здесь можно вспомнить и топологию, которая тоже изучает свойства тел и поверхностей (правда, несколько под другим углом зрения). С игрой, использующей пространственное расположение слов, вы уже познакомились (см. «Формальный кроссворд» – 1.3.4). Вот еще одна.

1.4.2. Королевская балда

Играют обычно двое. Расчерчивается квадрат 5 x 5 клеток, посередине пишется любое пятибуквенное слово.



В	Е	Н	О	К

Первый вариант: ходят по очереди. За каждый ход можно поставить в любую пустую клетку по соседству с буквой другую так, чтобы она вошла в состав слова. Его разрешается читать, продвигаясь только по смежным клеткам (прилегающим друг к другу стороной или углом), т. е. ходом шахматного короля. Дважды проходить через какую-то клетку или разрываться слово не должно. Какой длины оно получилось, столько очков записывает себе игрок (если можно прочесть сразу несколько слов, из них выбирается наибольшее). В приведенном примере первый игрок может заработать 4 очка, если припишет букву о над в – получится овен. Второй поставит д справа от этой о и сможет прочесть коневод (7 очков) и т. д. Выигрывает тот, кто к моменту заполнения всего квадрата наберет большую сумму (если, конечно, каждый сделал одинаковое количество ходов).

В игре необходимо учитывать последствия собственных ходов, чтобы не предоставлять противнику хорошие возможности (как это произошло с первым игроком в нашем примере). Можно даже проводить комбинации, рассчитывая на несколько ходов вперед.

В более свободных правилах игры разрешается читать одну и ту же клетку несколько раз. Это значит, например, что в четырех смежных буквах

К	О
Л	Т

можно увидеть и колокол, и околоток.

Во втором варианте проводят игру иначе, заполнив заранее все клетки (годятся и квадраты других размеров – 4 x 4, 6 x 6). Делать это нужно случайным образом – скажем, один игрок указывает клетку, а другой не глядя называет букву, которую нужно туда поставить. Выигрывает тот, кто найдет больше разных слов в таком квадрате. Опытный игрок, конечно, предпочтет договориться о том, чтобы искать слова не менее 4–5 букв длиной.

Существует и более тонкий третий вариант, известный под названием «дамский квадрат». В нем при подсчете очков учитывается не только длина слова, но и «цена» составляющих его букв. В качестве цены можно использовать уже знакомые нам числовые соответствия – например, порядковый номер буквы. Другой способ – учитывать частоту употребления буквы: чем реже она встречается в текстах, тем больше очков приносит (см. игру «Крестословица» – 1.3.3).

Задание 1.4.2.1. Подберите начальное слово и сыграйте партию в «Королевскую балду» сами с собой так, чтобы за все двадцать ходов набрать в сумме как можно больше очков.

О влиянии языка на логику говорилось в главе 1.1. Неудивительно, что у многих языковых игр есть логическая подоплека.

1.4.3. Коровы

Играют вдвоем. Каждый задумывает слово из пяти разных букв. Затем игрок называет сопернику другие пятибуквенные слова, и тот должен отвечать, сколько букв в названном слове совпадает с задуманными буквами (сколько раз совпадающая буква повторяется в названном слове, столько раз ее считают). Побеждает тот, кто назовет слово соперника за меньшее количество ходов.

Игра упрощается, если применять четырех- или трехбуквенные слова.

Прототип «Коров» – логическая игра «Быки и коровы» (другое название – «Ум мастера»). В ней скрывается от соперника не слово, а набор из четырех (реже пяти) элементов разных типов (это могут быть цифры, буквы, разноцветные фишки). Определяют его, выставляя пробные наборы. Партнер выдает сигнал «бык» на каждое совпадение по типу и позиции и сигнал «корова», если в пробном наборе встретился один из скрытых элементов, но расположен он иначе.

Если используется слово, а не произвольный набор символов, то надобность в «быках» отпадает – сведения о составе слова можно получить и от одних «коров», а чтобы найти правильный порядок букв, достаточно разгадать анаграмму. Более того, далеко не из всякого набора букв можно составить слово, а это значит, появляется дополнительный логический фильтр для отбрасывания заведомо неправильных вариантов.

Задание 1.4.3.1. Задумано трехбуквенное слово. Из него две буквы содержатся в слове род и одна – в слове оса. Не пользуясь бумагой, за одну минуту определите задуманное.

Задание 1.4.3.2. Даны пять слов: мушка, шутка, смола, катер, сурок. В каждом из них присутствуют по две буквы из загаданного пятибуквенного слова. Определите его.

Представлена в лингвистических играх и такая комбинация, как логика + геометрия. Известно большое количество игр с фигурами или фишками, переставляемыми по определенным правилам: шахматы, шашки, го, нарды и т. п. При желании, в любую из этих игр можно сделать лингвистическую инъекцию: пусть, скажем, каждой клетке поля соответствует определенная буква или набор букв так, чтобы ходами фигур задавать цепочки-слова (вспомним традиционную головоломку – ходом шахматного коня прочесть зашифрованную на поле запись). Можно сделать наоборот: закрепить буквы за фигурами и рассматривать их комбинации, возникающие в игре. Возможны и другие варианты – здесь открывается простор для творчества конструкторов игр.

Предлагаем одну довольно простую логико-геометрически-лингвистическую игру.

1.4.4. Чехарда

Это игра для двоих. Нужно расчертить игровое поле 4 x 4 клетки и вырезать из картона 8 фишек. Каждый придумывает четырехбуквенную анаграмму – два слова, которые составляются из одного и того же набора букв, – и записывает на четырех фишках по букве. Тот, кому выпало по жребию начинать игру, расставляет фишки в нижнем ряду поля, образуя одно слово анаграммы, второе пишет над самым верхним рядом. Соперник обводит кружками все буквы на своих фишках (чтобы они стали «черными») и составляет из них слово в верхнем ряду; анаграмма этого слова пишется под нижним рядом. Получается, например, такая начальная позиция:

Для обозначения ходов здесь приведена еще и шахматная нотация вертикалей и горизонталей, необязательная в игре.

Делающий очередной ход передвигает свою фишку на одну пустую клетку вперед прямо или по диагонали. Если какая-либо из этих двух или трех клеток занята другой фишкой (неважно, чьей), через нее можно перепрыгнуть на пустую клетку вперед или по диагонали. Ходить назад или вбок не разрешается. После каждого хода игрок пытается составить слово, передвигаясь от буквы к букве (должна быть обязательно прочитана и та, которую он только что передвинул). Продвигаться при чтении можно через любые смежные (имеющие общую сторону или вершину) клетки, одну и ту же клетку можно проходить сколько угодно раз, в том числе и подряд. Самое длинное из всех слов, которые удалось составить, игрок записывает для себя. Повторять использованные ранее слова нельзя. Когда один из игроков расставляет все свои фишки на последней линии, у него должно составиться записанное там слово. Если сделано четное количество ходов и кто-то уже достиг последней линии, второй выбывает из игры, а первый ходит за него, приписывая получающиеся слова себе. Побеждает тот, у кого суммарное количество букв в записанных словах будет больше. Пример партии с приведенной выше начальной позицией:

1-й игрок (рост) 2-й игрок (пика)

D1–C2 ротор 5 D4–C3 стаккато 8

B1–B2 статор 6 A4–B3 стопка 6

C1–D2 пастор 6 C4–A2 рокот 5

C2–A4 тип 3 C3–C2 пасс 4

A1–C3 порок 5 A2–A1 окорок 6

D2–D3 пирс 4 B4–A3 копи 4

B2–B4 ропот 5 B3–B2 пара 4

C3–C4 рот 3 A3–A2 пики 4

D3–D4 торс 4 B2–C1 папа 4

У первого игрока всего 41 буква против 45 у второго, но он уже провел к финишу все свои фишки, поэтому, доканчивая игру двумя ходами за второго, C2–D1 па и A2–B1 кипа, он выигрывает с перевесом в 2 буквы.

Задание 1.4.4.1. Разработайте идею игры «Лингвистические шахматы».

Глава 1.5

ХОББИ ЭДГАРА ПО

Язык – сокровищница парадоксов. Один из них заключается в том, что с помощью слов можно искажать и скрывать свои мысли. Во-первых, сплошь и рядом человек делает это против своей воли, не умея подобрать нужные, соответствующие случаю слова. Во-вторых, у каждого средства выражения есть недостатки и ограничения, и даже тот, кто в совершенстве владеет языком, абсолютной точности в описании образов никогда не достигает. Этой теме немало стихов посвятил Ф. Тютчев. Крылатой стала его строка: «Мысль изреченная есть ложь». В-третьих, у каждого человека язык все-таки во многом индивидуален, и нередко люди, говорящие, казалось бы, на одном наречии, совершенно не понимают друг друга. Что уж говорить о разных языках? Не зря русское название западного соседа «немец» произошло от слова «немой», т. е. не могущий изъясняться, произносящий бессмысленные звуки. Кстати говоря, американцы во время последней мировой войны использовали для передачи секретных сообщений один из малоизвестных индейских языков, и немецким дешифровщикам не удавалось их понять.

Искусство искажать слова до неузнаваемости зародилось в самые древние времена, поскольку всегда существовала необходимость в секретах. Зашифровывание – по существу формальная операция, и поскольку количество математических преобразований неисчислимо, шифров придумано великое множество. Конечно, популярность завоевали те из них, которые просты и удобны в обращении. Однако с появлением машин – вначале специальных шифровальных, а потом и универсальных вычислительных – громоздкость операций уже не препятствие для того, кто хочет запутать следы. Но каждое техническое усовершенствование – палка о двух концах. Те же компьютеры стали могучим средством в руках дешифровщиков. Поэтому не прекращается соревнование изобретателей новых шифров и специалистов по их раскрытию.

Шифры всегда волновали воображение людей, за ними скрывались таинственные события, клады, интриги и неожиданности. Игры с тайнописью очень увлекательны, особенно если сопровождают другую деятельность – обучение, отдых или работу.

1.5.1. Шифры

Играть можно двумя способами.

В первом варианте зашифровывают и расшифровывают тексты по известным ключам, получая удовольствие или пользу от этого увлекательного процесса.

Во втором варианте ищут неизвестный ключ к шифру. Задача эта чрезвычайно сложна для неквалифицированного дешифровщика, а то и вообще невыполнима. Поэтому в игре иногда используют подсказки.

Один из видов подсказки – употребление закодированного и открытого текстов вместе. По их сопоставлению нужно догадаться о способе шифровки. Между прочим, с помощью такой подсказки были некогда расшифрованы египетские иероглифы: обнаружили запись одного и того же текста на трех языках и появилась возможность сравнить известное с неизвестным. Перечислим некоторые шифры, удобные для игры.

A. Страница

Ключом служит любая печатная страница. На ней находят первую букву шифруемого текста и записывают через тире: номер строки – номер слова – номер буквы (часть слова до или после переноса считается отдельным словом). Со второй и последующими буквами поступают так же. Удобнее использовать страницу, если строчки на ней предварительно пронумерованы.

Прочесть текст просто, если знаешь, какой страницей и какого издания воспользоваться.

Б. Решетка

На листке бумаги в клеточку вырезаются отдельные клетки. Этот листок-ключ накладывают на бумагу для сообщения (лучше тоже в клеточку) и в прорезях записывают текст – по букве в клетке. Затем решетку снимают и на оставшихся чистыми местах пишут любые буквы.

Прочесть зашифрованный текст очень просто, если наложить на него решетку-ключ.

B. Квадрат

Недостаток предыдущего способа – нерациональное использование бумаги. Желательно весь листок заполнить буквами текста вперемешку. Для этого применяют специальную решетку.

Делается она так. Из бумаги вырезают квадрат, разбивают на четное количество клеток, а в центр втыкают кнопку или булавку. Помечают крестиком любую клетку. Находят еще 3 клетки, которые совпадают с выбранной при последовательных поворотах квадрата на 90° вокруг центра (их помечают точками). На любую из свободных клеток ставится следующий крестик, точки за ним и т. д. до тех пор, пока не будет заполнен крестиками и точками весь квадрат. Правильность заполнения можно проверить, подсчитав крестики: если сторона квадрата n клеток, то крестиков должно быть n²/4.

Вот, например, что может получиться при n = 6:

Затем делаются вырезы (некоторые – закругленные, чтобы квадрат не распался) там, где стоят крестики; помечается верх – и ключ к шифру готов. Его можно наложить на бумагу, заполнить вырезы буквами секретного текста, затем повернуть, не сдвигая центр, на четверть оборота по часовой стрелке и продолжить запись. Так можно сделать еще дважды, пока не будет заполнено буквами все пространство под ключом (если длина текста меньше n² букв, в конце ставят произвольные слова).

Читается криптограмма наложением ключа и его поворотами.

Г. Символы

Каждая буква алфавита обозначается символом, придуманным или уже существующим, рисунком, знаком, числом или другой буквой того же алфавита. Зашифровывается текст заменой всех букв в нем соответствующими символами.

Для расшифровки служит таблица символов.

Д. Сдвиг

В частном случае шифра Г, когда вместо одной буквы алфавита пишут другую, обычно используют простой сдвиг на единицу: заменяют а на б, б на в и т. д., а я на а. Величина сдвига может быть и больше единицы.

Е. Коды

Если каждой букве будет соответствовать какое-нибудь число, например АСКИ-код, о котором шла речь в предыдущей главе, это будет частным случаем шифра Г. Но с числами, как известно, можно проделывать различные математические операции. Если, к примеру, каждый третий код увеличить на единицу, а каждый второй на единицу уменьшить, это существенно осложнит дешифровку. Возможны и другие преобразования.

Ж. Палочка

На круглую палочку наматывают полоску бумаги и пишут текст вдоль оси этой палочки. Чтобы прочесть тайнопись, нужна палочка такого же диаметра.

К числу наиболее трудных относится шифр «страница». Очень сложны также «решетка» (если размер решетки велик) и «квадрат». Можно запутать дешифровщиков и с помощью «кодов». А вот шифр «символы», вопреки распространенному мнению, не такой уж сложный. Эдгар По, большой любитель таинственного, увлекался криптографией и был специалистом в этой области. Через газету он объявил однажды, что прочитает любую шифровку, основанную на замене букв. Многие приняли вызов, но никому не удалось составить текст, который нельзя было бы разгадать. Процесс раскрытия подобного шифра описан в рассказе Э. По «Золотой жук». Основное, что требуется для раскрытия ключа, – анализ частот символов и сопоставление их с общеизвестными частотами букв. Тем более прост «сдвиг»: если установлено, что применяется именно этот шифр, найти величину сдвига можно легко, всего за несколько минут. Столь же быстро разгадывается и «палочка» – проверкой на цилиндрах разных диаметров.

Лингвистическая игра – это не обязательно ограниченное во времени действие, изолированное от реальной жизни. На примере «Шифров» видно, что игровым можно сделать обмен любой письменной информацией. По такому же принципу – игрового засекречивания – можно вести и устную беседу. Способы, применяемые в этом случае, гораздо проще настоящих шифров: при разговоре нет времени обдумывать громоздкие преобразования; обычно делают перестановки, добавления и изменения слогов.

1.5.2. Тайный язык

Для игры можно использовать следующую таблицу:

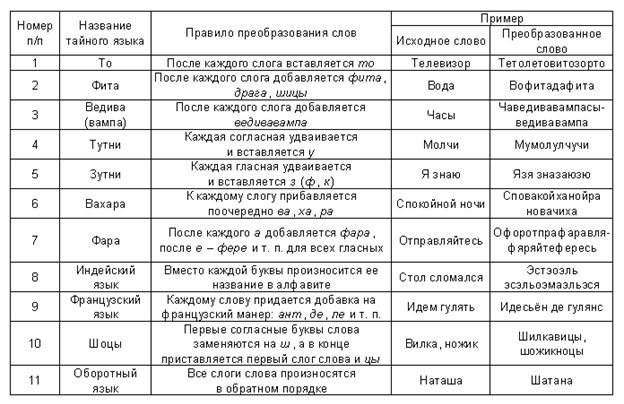
Участники игры договариваются, что в некоторых ситуациях (например, при разговоре на определенную «секретную» тему) каждое слово в ключевых фразах разговора должно известным образом изменяться. Это игра не на выигрыш, а на сотрудничество – поддержание тайной общности.

Преобразования поначалу кажутся сложными, но после непродолжительной тренировки оказывается, что это не так. Все приведенные примеры взяты из реальных детских тайных языков. Можно указать и конкретных литературных героев, которые изъясняются таким способом. Например, персонажи сказки Т. Янссон «Шляпа волшебника» (перевод В. Смирнова) Тофсла и Вифсла разговаривают так:

– Таксла или инаксла тут готовслят кофсла.

– Кто-то идетсла! Тихо сидисла!

Подобные тайные языки (их называют «поросячьей латынью») основаны на чисто формальных преобразованиях общеупотребительных слов и не имеют почти ничего общего с жаргоном, о котором речь пойдет в главе 3.2.